Éléments de statistiques
Éléments de statistiques
- I Indicateurs de position
- II Indicateur de dispersion
- III Effectif et fréquence
- IV Diagrammes
- V Exercices
Définition : [Statistiques d'après Encyclopedia Universalis]
Le mot statistique désigne à la fois un ensemble de données d'observations et l'activité qui consiste dans leur recueil, leur traitement et leur interprétation.
I Indicateurs de position
- I Indicateurs de position
- II Indicateur de dispersion
- III Effectif et fréquence
- IV Diagrammes
- V Exercices
I-1 Moyenne d'une série à valeurs individuelles
I-2 Moyenne d'une série à valeurs affectées d'un coefficient
Éléments de statistiques
→ I Indicateurs de position
I-1 Moyenne d'une série à valeurs individuelles
- I Indicateurs de position
- II Indicateur de dispersion
- III Effectif et fréquence
- IV Diagrammes
- V Exercices
Soit la série statistique suivante qui est la liste des notes d'un élève lors d'un trimestre de sa scolarité :
Pour calculer la moyenne d'une série statistique à valeurs individuelles, on fait la somme de toutes les valeurs et on divise par le nombre de valeurs.
Ici, on a donc :
Une valeur approchée de la moyenne est de
.
| Notes | 12 | 7.5 | 11.5 | 6.5 | 13 | 8.5 | 17 | 8.5 | 17.5 |
Pour calculer la moyenne d'une série statistique à valeurs individuelles, on fait la somme de toutes les valeurs et on divise par le nombre de valeurs.
Ici, on a donc :
| = | ||
| = | ||
| = |
Exercice :
Moyenne - Cliquer
Éléments de statistiques
→
I Indicateurs de position
→ I-1 Moyenne d'une série à valeurs individuelles
I-2 Moyenne d'une série à valeurs affectées d'un coefficient
- I Indicateurs de position
- II Indicateur de dispersion
- III Effectif et fréquence
- IV Diagrammes
- V Exercices
Le professeur décide d'affecter un coefficient aux différentes notes obtenues par l'élève (ou un autre élève), on a alors une nouvelle série statistique, que l'on peut expliciter dans le tableau suivant :
Pour calculer cette moyenne on fait le produit de chaque valeur et du coefficient qui lui est affecté. On fait alors la somme de tous ces produits, puis on divise par la somme des coefficients. Ici, on a donc :
Une valeur approchée de la moyenne est de
.
| Notes | 8.5 | 13.5 | 8 | 12.5 | 14.5 | 17 | 8.5 | 14 |
| Coeff. | 3 | 1 | 2 | 2 | 2 | 1 | 1 | 2 |
Pour calculer cette moyenne on fait le produit de chaque valeur et du coefficient qui lui est affecté. On fait alors la somme de tous ces produits, puis on divise par la somme des coefficients. Ici, on a donc :
| = | ||
| = | ||
| = |
Exercice :
Moyenne avec coefficients - Cliquer
Éléments de statistiques
→
I Indicateurs de position
→ I-2 Moyenne d'une série à valeurs affectées d'un coefficient
I-3 Médiane
- I Indicateurs de position
- II Indicateur de dispersion
- III Effectif et fréquence
- IV Diagrammes
- V Exercices
Définition : [Médiane]
On appelle médiane d'une série, un nombre tel qu'il y a autant de valeurs inférieures à ce nombre que de valeurs supérieures.
Premier cas : on prend une série statistique, où les valeurs sont rangées par ordre croissant. Il y a un nombre impairs de valeurs.
Considérons la série suivante qui a 9 éléments : .
On ordonne cette série par ordre croissant des valeurs : .
On peut alors répartir cette série en trois parties de éléments.
La valeur médiane est : 40.
Deuxième cas : on prend une série statistique, où les valeurs sont rangées par ordre croissant. Il y a un nombre pairs de valeurs.
Considérons la série suivante qui a 6 éléments : .
On ordonne cette série par ordre croissant des valeurs : .
On peut alors répartir cette série en deux parties de même effectif 3 et 3 éléments. On fait alors la moyenne des deux valeurs qui partagent la série.
On fait alors la moyenne de la valeur de rang 3 (qui vaut 57) avec la valeur de rang 4 (qui vaut 57). La valeur médiane est : (57+57)/2=57.
Éléments de statistiques
→
I Indicateurs de position
→ I-3 Médiane
II Indicateur de dispersion
- I Indicateurs de position
- II Indicateur de dispersion
- III Effectif et fréquence
- IV Diagrammes
- V Exercices
Éléments de statistiques
→ II Indicateur de dispersion
II-1 Étendue
- I Indicateurs de position
- II Indicateur de dispersion
- III Effectif et fréquence
- IV Diagrammes
- V Exercices
Définition : [Étendue]
L'étendue d'une série statistique est la différence entre la plus grande et la plus petite des valeurs du caractère.
Dans la série statistique suivante :
99,42,41,24,78,84,19,36,15,18.
La plus grande valeur est 99, la plus petite est 15. L'étendue de cette série est donc
Exercice :
- Médiane 1
- Médiane 2
- Moyenne et étendue
- Moyenne avec coefficients et étendue
Éléments de statistiques
→
II Indicateur de dispersion
→ II-1 Étendue
III Effectif et fréquence
- I Indicateurs de position
- II Indicateur de dispersion
- III Effectif et fréquence
- IV Diagrammes
- V Exercices
Définition : [Effectif]
On appelle effectif d'une valeur du caractère (ce que l'on est en train d'étudier), le nombre de fois qu'apparaît cette valeur.
Voici une série statistique :
On peut alors dresser le tableau des effectifs des valeurs de cette série :
Voici une série statistique :
| Série | 3 | 3 | 4 | 6 | 5 | 7 | 1 | 4 | 1 | 3 | 3 | 4 | 7 | 1 | 3 | 7 | 5 | 2 | |
| Valeurs | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Effectifs | 0 | 3 | 1 | 5 | 3 | 2 | 1 | 3 |
Définition : [Fréquence]
On appelle fréquence d'une valeur du caractère (ce que l'on est en train d'étudier), le quotient de l'effectif de cette valeur par l'effectif total.
La fréquence est un nombre, elle vérifie : , et on a :
On utilise aussi la fréquence en pourcentage, ou pourcentage :
Remarque :
Les lignes "Effectifs" et "Fréquence" du tableau des effectifs des valeurs, sont proportionnelles. On peut calculer le total des effectifs, et on sait que le total des fréquences est égal à 1 (ou à 100 si la fréquence est exprimée en pourcentage.) puis on complète le tableau en utilisant les propriétés des tableaux de proportionnalité.
On peut alors compléter le tableau des effectifs des valeurs de cette série :
| Valeurs | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | Total |
| Effectifs | 0 | 3 | 1 | 5 | 3 | 2 | 1 | 3 | 18 |
| Fréquences | 0 | 0.167 | 0.056 | 0.278 | 0.167 | 0.111 | 0.056 | 0.167 | 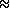 1 1 |
| Pourcentages | 0 | 16.7 | 5.6 | 27.8 | 16.7 | 11.1 | 5.6 | 16.7 | 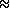 100 100 |
Exercice :
- Répartition et fréquences - Cliquer
- Répartition, fréquences et regroupement - Cliquer
Éléments de statistiques
→ III Effectif et fréquence
IV Diagrammes
- I Indicateurs de position
- II Indicateur de dispersion
- III Effectif et fréquence
- IV Diagrammes
- V Exercices
Éléments de statistiques
→ IV Diagrammes
IV-1 Diagrammes en bâtons
- I Indicateurs de position
- II Indicateur de dispersion
- III Effectif et fréquence
- IV Diagrammes
- V Exercices
Les diagrammes en bâtons, dits aussi diagrammes en barres si on donne une largeur aux bâtons, utilisent les valeurs du caractère (les notes) en abscisse et les valeurs de l'effectif (ou du coefficient) en ordonnée.
Voici une série statistique :
| Série | 5 | 5 | 1 | 4 | 1 | 4 | 6 | 5 | 4 | 4 | 6 | 5 | 1 | 2 | 0 | 0 | |||
| Valeurs | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| Effectifs | 2 | 3 | 1 | 0 | 4 | 4 | 2 |
Éléments de statistiques
→
IV Diagrammes
→ IV-1 Diagrammes en bâtons
IV-2 Diagrammes circulaires
- I Indicateurs de position
- II Indicateur de dispersion
- III Effectif et fréquence
- IV Diagrammes
- V Exercices
Les diagrammes circulaires : il y a proportionnalité entre les mesures des angles et l'effectif associé à un caractère.
Voici une série statistique :
| Série | 4 | 3 | 5 | 2 | 2 | 2 | 5 | 1 | 1 | 4 | 1 | 1 | 0 | 0 | 4 | 4 | 3 | 4 | 4 |
| Valeurs | 0 | 1 | 2 | 3 | 4 | 5 |
| Effectifs | 2 | 4 | 3 | 2 | 6 | 2 |
| Angles | 37.8 | 75.96 | 56.88 | 37.8 | 113.76 | 37.8 |
Éléments de statistiques
→
IV Diagrammes
→ IV-2 Diagrammes circulaires
IV-3 Histogrammes
- I Indicateurs de position
- II Indicateur de dispersion
- III Effectif et fréquence
- IV Diagrammes
- V Exercices
Quand les valeurs sont trop nombreuses ou trop continues, la taille de 500 personnes par exemple, on utilise un regroupement en classe, le diagramme associé est appelé histogramme. Pour estimer la moyenne dans de tels problèmes, on utilise le centre de classe comme représentant de la classe. Pour nous, nous ne construirons des histogrammes que quand les classes ont la même amplitude.
Les tailles arrondies à un nombre entier de centimètres des 50 garçons d'un club de football sont les suivantes :
| 160 | 160 | 160 | 160 | 160 | 160 | 160 | 160 | 160 | 160 |
| 160 | 160 | 160 | 160 | 160 | 160 | 160 | 160 | 160 | 160 |
| 160 | 160 | 160 | 160 | 160 | 160 | 160 | 160 | 160 | 160 |
| 160 | 160 | 160 | 160 | 160 | 160 | 160 | 160 | 160 | 160 |
| 160 | 160 | 160 | 160 | 160 | 160 | 160 | 160 | 160 | 160 |
L'analyse statistique de ces données permet de remplir le tableau suivant :
| Tailles | ||||||
|---|---|---|---|---|---|---|
| Effectif | 0 | 0 | 0 | 0 | 0 | 0 |
| Fréquence | NaN | NaN | NaN | NaN | NaN | NaN |
L'amplitude des classes (différence entre la plus grande et la plus petite des valeurs de l'intervalle) est de 5. Les centres des classes sont 162.5,167.5,172.5,177.5,182.5,187.5 ; ils sont utiles si on souhaite calculer une valeur approchée de la moyenne.
Éléments de statistiques
→
IV Diagrammes
→ IV-3 Histogrammes
V Exercices
- I Indicateurs de position
- II Indicateur de dispersion
- III Effectif et fréquence
- IV Diagrammes
- V Exercices
Exercice :
- Étude de taille - Cliquer
- Effectifs et pourcentages - Cliquer
- Statistiques et pourcentages - Cliquer
- Diagrammes circulaires et pourcentages - Cliquer
- Angles et pourcentages - Cliquer
Éléments de statistiques
→ V Exercices