Fractions rationnelles
Guide
- Définition d'un élément simple
- Théorème
- Théorème général de décomposition en éléments simples sur R
- Calcul de la partie entière
- Calcul de la partie polaire
-
Exercices : Exercices de calcul : (de plus en plus de calculs !)
- Pôles réels simples
- Pôles réels simples
- Pôles réels simples et partie entière
- Pôles réels simples et partie entière
- Pôles réels et complexes
- Partie entière, pôles réels et complexes
- Reconnaître
- Reconnaître
- Reconnaître
- Algorithme général
Définition d'un élément simple
On appelle fraction rationnelle (sur
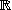 ) toute fonction
définie par une relation de la forme
) toute fonction
définie par une relation de la forme
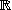 ) toute fonction
définie par une relation de la forme
) toute fonction
définie par une relation de la forme
où et sont des polynômes à coefficients réels.
Par exemple,
ou encore
On note l'ensemble des fractions rationnelles sur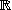 .
.
On appelle élément simple de
une fraction rationnelle d'un des deux types suivants :
- type "racine réelle" :
avec
et
des nombres réels et
un entier.
Cet élément simple a pour numérateur une constante et pour dénominateur une puissance d'un polynôme où est un réel. - type "racines complexes conjuguées" : où , sont des réels, où , sont des réels vérifiant et où est un entier naturel non nul. Cet élément simple a pour numérateur un polynôme de degré 1 et pour dénominateur une puissance d'un trinôme sans racine réelle.
Théorème
Théorème
Théorème : Toute fraction rationnelle sur 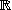 s'écrit de façon unique comme somme d'un polynôme (appelé partie entière) et d'éléments simples (appelé partie polaire) dont le type est déterminé par le dénominateur de la fraction rationnelle qu'on décompose.
s'écrit de façon unique comme somme d'un polynôme (appelé partie entière) et d'éléments simples (appelé partie polaire) dont le type est déterminé par le dénominateur de la fraction rationnelle qu'on décompose.
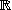 s'écrit de façon unique comme somme d'un polynôme (appelé partie entière) et d'éléments simples (appelé partie polaire) dont le type est déterminé par le dénominateur de la fraction rationnelle qu'on décompose.
s'écrit de façon unique comme somme d'un polynôme (appelé partie entière) et d'éléments simples (appelé partie polaire) dont le type est déterminé par le dénominateur de la fraction rationnelle qu'on décompose.
Cela sera précisé avec les techniques pour les obtenir dans quelques cas particuliers que l'on conseille de regarder d'abord.
Des techniques ou algorithmes plus systématiques sont expliquées d'autre part. Elles sont facilement programmables. Il faut quand même insister sur le fait qu'il y a derrière un problème difficile dont on ne parle pas : trouver les pôles et en particulier les pôles simples de la fraction rationnelle , c'est-à-dire les racines du polynôme .
Théorème général de décomposition en éléments simples sur R
Théorème général de décomposition en éléments simples sur R
Soit une fraction rationnelle avecavec les u i des réels, les p j et les q j des réels tels que et les n i et les m j des entiers strictement positifs.
Théorème : Il existe une et une seule décomposition en éléments simples de P(x)/Q(x) et elle est de la forme :
avec
- E un polynôme nul ou de degré égal à deg(P)-deg(Q),
- les Ai,l, les Bj,k et les Cj,k des réels
Calcul de la partie entière
Proposition :
La partie entière
de la fraction rationnelle
est le quotient de
par
dans la division euclidienne de
par
.
Ainsi :
avec ) et
On est alors ramené au cas où le degré du numérateur est strictement inférieur à celui du dénominateur.
Comment faire la division euclidienne ?
Division euclidienne
Faisons la division euclidienne sur des exemples. N'hésitez pas à recommencer . Et allez voir ensuite comment poser la division euclidienne .
Prenons =, = alors :
=()() +()
c'est-à-dire avec E(x) = et R(x) = . Bien remarquer que le degré de R qui est est strictement inférieur à NaN. Effectuons la division : on écrit avec P=P0 :P0(x)= Q +
Le degré de est strictement plus petit que celui de . Il est aussi strictement inférieur à celui de Q, on a donc fini ; le reste est P1= ; le quotient est obtenu en ajoutant les monômes en rouge.
En général, on pose la division euclidienne de la manière suivante
Calcul de la partie polaire
On suppose maintenant que l'on cherche à décomposer la fraction rationnelle P(x)/Q(x) en éléments simples quand deg(P) < deg(Q). Dans cette situation, la partie entière est nulle.On étudie en détail les cas particuliers suivants et on précise dans ces cas particuliers le théorème
Le degré de Q est 3 et celui de P est inférieur ou égal à 2
Soit une fraction rationnelle P(x)/Q(x) telle que le degré de Q est égal à 3 et le degré de P est au plus égal à 2. Suivant les racines du dénominateur, sa décomposition prendra l'une des formes suivantes où a, b, c, A, B, C sont des réels :- Si Q(x) admet 3 racines simples distinctes réelles
Pour calculer A : on utilise la Technique 1On multiplie l'égalité donnant la forme de la décomposition rationnelle en éléments simples par (x - u), puis on donne à la valeur . On obtient immédiatement .
et de même pour B et C
Exemple - Si Q(x) admet 1 racine simple et 1 racine double réelle :
TechniqueOn calcule A et C par la technique 1 et la technique 2 donne la valeur de A + B. Technique 1On multiplie l'égalité ci-dessus par (x - v)2, puis on donne à x la valeur v. On obtient immédiatement le coefficient de .
Technique 1On multiplie l'égalité donnant la forme de la décomposition rationnelle en éléments simples par (x - u), puis on donne à la valeur . On obtient immédiatement .Technique 2On multiplie l'égalité ci-dessus par x et on fait tendre x vers l'infini.
Exemple - Si Q(x) admet 1 racine simple réelle et 2 racines complexes conjuguées :
TechniqueOn calcule- A par la
technique 1
On multiplie l'égalité donnant la forme de la décomposition rationnelle en éléments simples par (x - u), puis on donne à la valeur . On obtient immédiatement .
-
B par la
technique 2
On multiplie l'égalité ci-dessus par x et on fait tendre x vers l'infini.
-
C par la
technique 3
L'égalité de décomposition est vraie pour tout x ; en donnant à x une valeur numérique, on obtient une relation entre les coefficients des numérateurs.
Exemple - A par la
technique 1
- Si Q(x) admet 1 racine triple réelle :
TechniqueOn peut calculer les trois coefficients , et
- soit par les techniques précédentes
-
soit en faisant le changement de variable
.
Le degré de
est au plus 2 donc
s'écrit ay2 + by + c.
En divisant par y3=(x-u)3, on obtient
et par unicité de la décomposition, on en déduit , et .
Exemple
Considérons la fraction rationnelle
On cherche A, B et C tels que
- Pour calculer A, on multiple par , on obtient donc et on prend la valeur en x=-3, donc A = .
- Pour calculer B, on multiple par , on obtient donc et on prend la valeur en x=-6, donc B = .
- Pour calculer C, on multiple par , on obtient donc et on prend la valeur en x=11, donc C = .
Exemple
Considérons la fraction rationnelleOn cherche A et B tels que
- Pour calculer A, on multiple par , on obtient donc et on prend la valeur en x = 2, donc A =.
- Pour calculer C, on multiple par ()2, on obtient donc et on prend la valeur en x = -5, donc C =.
- Pour calculer B, on multiple par x et on fait tendre x vers l'infini : on obtient donc 0 = A + B= + B, donc B =.
Exemple
Considérons la fraction rationnelle
On cherche A, B et C tels que
- Pour calculer A, on multiplie par , on obtient donc et on prend la valeur en x = -5, donc A =.
- Pour calculer B, on multiplie par x et on fait tendre x vers l'infini : on obtient donc -3= A+B=+B, donc B =.
- Pour calculer C, on prend une valeur particulière autre que le pôle -5, par exemple x = 0 : d'où C =.
Exemple
Considérons la fraction rationnelle
On cherche A, B et C tels que
On fait le changement de variables x =. On a donc
Donc
Algorithme général
Pour des exemples de décomposition de la fraction P(x)/Q(x), voir Exemple- On calcule la partie entière en faisant la division euclidienne de P par Q
- On calcule la partie polaire de la décomposition
en éléments simples correspondant à un pôle
u de multiplicité m.
La fraction rationnelle s'écrit
avec Q1(u) non nul.
On fait un développement limité de
P/Q1 en
x = u à l'ordre m :
(en fait H est une fraction rationnelle de la forme P1/Q1 et donc n'ayant pas de pôle en x=u). On a donc
et la partie polaire de la décomposition en éléments simples est exactement - On fait de même pour tous les pôles.
- Dans le cas où les pôles sont complexes, on peut se ramener à
la décomposition sur
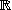 en regroupant les décompositions
correspondant à un pôle et à son conjugué.
en regroupant les décompositions
correspondant à un pôle et à son conjugué.