OEF Réseaux et flots
--- Introduction ---
Ce module regroupe pour l'instant 10 exercices sur les flots (définitions, flots complets).
Approvisionnement (modélisation)
Une société organise le transport de céréales des villes
vers les villes
. La disponibilité en tonnes des villes
est de
Les besoins en tonnes des villes
sont de
Le tableau suivant donne les capacités de transport, en tonnes, entre les villes :
On désire modéliser le problème. Pour cela, on introduit un graphe valué avec des capacités. Quelles capacités doit-on mettre sur chaque arête ?
Approvisionnement (résolution)
Une société organise le transport de céréales des villes
vers les villes
. La disponibilité en tonnes des villes
est de
Les besoins en tonnes des villes
sont de
Le tableau suivant donne les capacités de transport, en tonnes, entre les villes :
On a modélisé le problème par le graphe valué avec capacités suivantes. Déterminer les quantités à transporter de chaque ville d'origine vers chaque ville d'arrivée pour satisfaire au mieux la demande totale.
Saturation d'une chaîne
Voici un flot de à dans un graphe muni de capacités :
Cliquer sur les chaînes qui ne sont pas des chemins :
.
On se demande si le flot peut être amélioré en utilisant . Pour cela, on calcule pour chacun des arcs la capacité résiduelle : Peut-on améliorer le flot à l'aide de ? si oui, de combien ? sinon répondre 0.
Saturation d'un chemin
Voici un flot de à dans un graphe muni de capacités :
Cliquer sur les chemins du graphe :
.
On se demande si le flot peut être amélioré en utilisant . Pour cela, on calcule pour chacun des arcs la capacité résiduelle : Peut-on améliorer le flot à l'aide de ? si oui, de combien ? sinon répondre 0.
Rendre complet un flot donné
Le dessin suivant représente un flot muni de capacités. Il n'est peut-être pas complet. A vous de le rendre complet. La méthode utilisée ici est de saturer tous les arcs allant de
à
. La liste de tels arcs est la suivante :
L'arc
Les arcs
,
a été saturé.
ont été saturés.
Il reste encore à examiner les arcs
Il ne reste plus que l'arc à examiner.
L'arc est-il saturé ?
Répondre oui ou non.
Saturez l'arc en donnant les nouvelles valeurs du flot :
Construire un flot complet
Le dessin suivant représente un graphe muni de capacités. A vous de construire un flot complet en partant du flot nul. La méthode utilisée ici est de saturer tous les arcs allant de
à
. La liste de tels arcs est la suivante :
L'arc
Les arcs
,
a été saturé.
ont été saturés.
Il reste encore à examiner les arcs
Il ne reste plus que l'arc à examiner.
L'arc est-il saturé ?
Répondre oui ou non.
Saturez l'arc en donnant les nouvelles valeurs du flot :
Flot maximal et coupure
Le flot de
à
représenté ci-dessous est complet (saturé) pour les capacités indiquées :
Sa valeur est de
. La capacité minimale des coupures est obtenue pour la coupure suivante
(indiquer le sous-ensemble choisi contenant
) et vaut
.
La valeur du flot maximal possible est de
et le flot représenté
Coupure d'un flot
Calculer la capacité de la coupure 
du flot valué de
à
représenté ci-dessous :
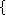
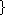Valeur d'un flot
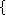
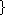Le dessin suivant représente un flot de
à
.
à condition de bien compléter le tableau suivant : La valeur du flot est
.
Définition d'un flot
Le dessin suivant représente un flot de
à
de valeur
à condition de bien compléter les valeurs manquantes :
The most recent version
Cette page n'est pas dans son apparence habituelle parce que
WIMS n'a pas pu reconnaître votre navigateur web.
Veuillez noter que les pages WIMS sont générées interactivement; elles ne
sont pas des fichiers
HTML ordinaires. Elles doivent être utilisées interactivement EN LIGNE.
Il est inutile pour vous de les ramasser par un programme robot.
- Description: collection d'exercices sur la recherche de flot maximum. interactive exercises, online calculators and plotters, mathematical recreation and games
- Keywords: interactive mathematics, interactive math, server side interactivity, operational_research, graph,algorithmics,informatics, maximum_flow, scheduling